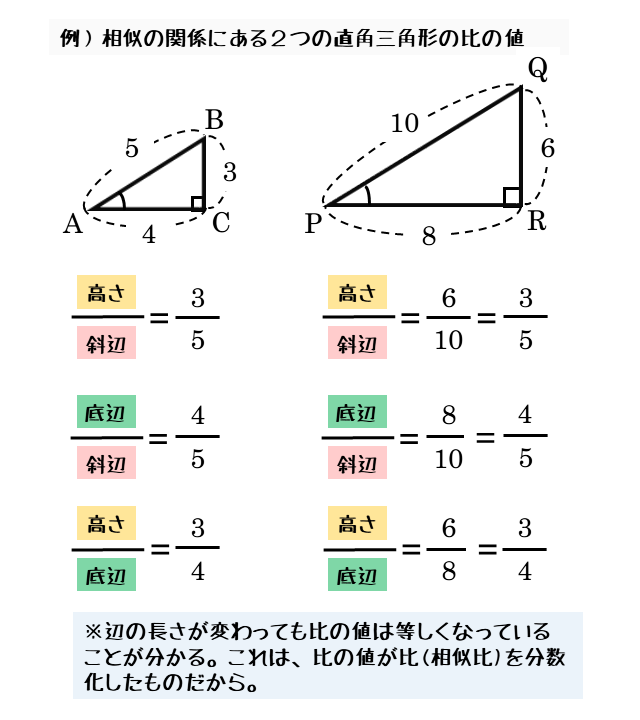
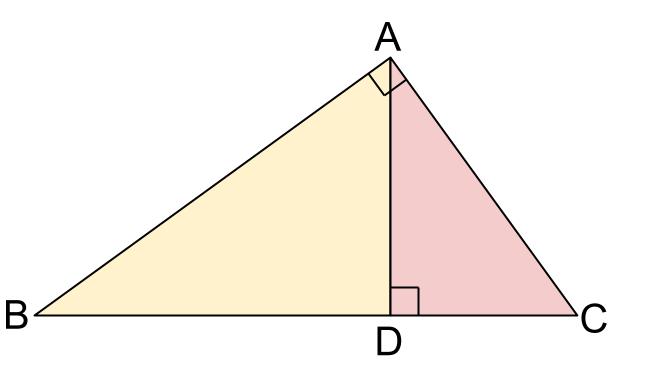
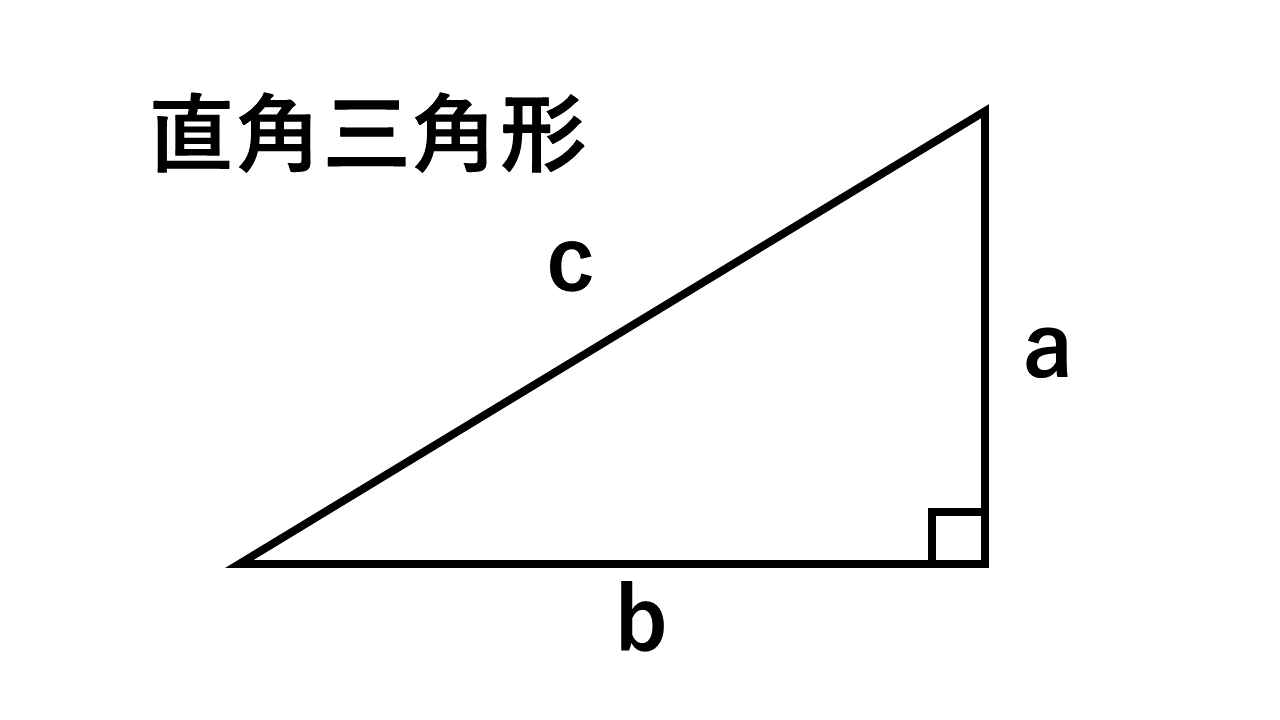
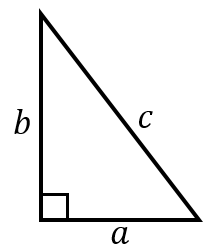
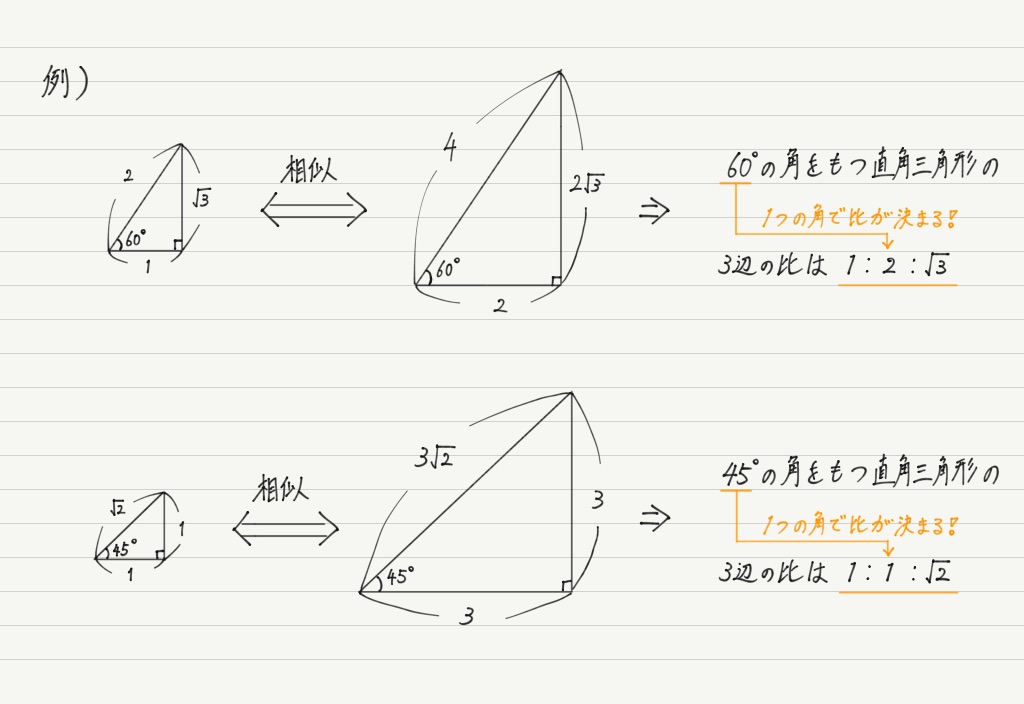
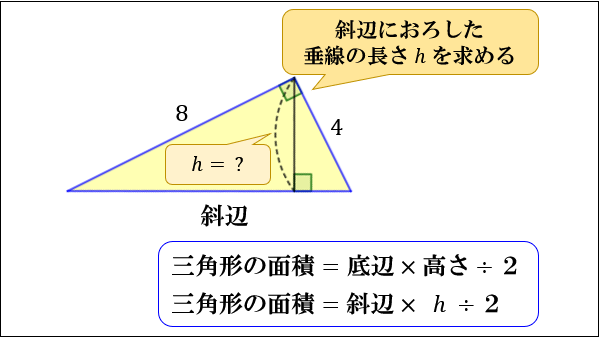
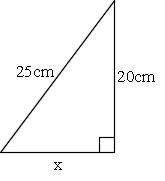
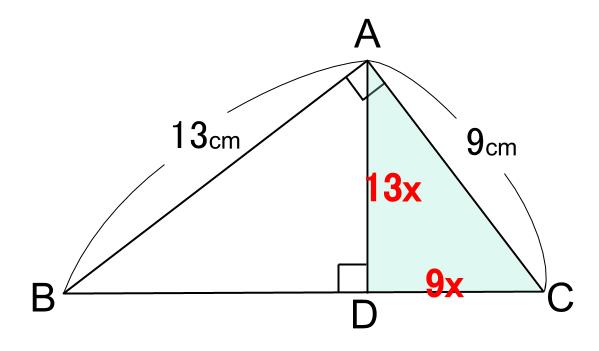
直角三角形の相似 相似の証明でも取り扱った「直角三角形の相似」です。 このページでは辺の長さや比を求めていきましょう。 相似な直角三角形が現れる図形として、最重要・最頻出のものを扱い
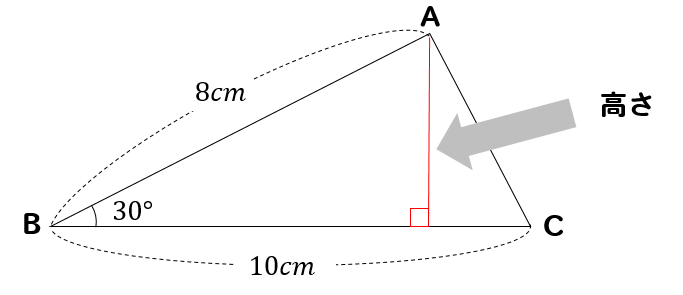
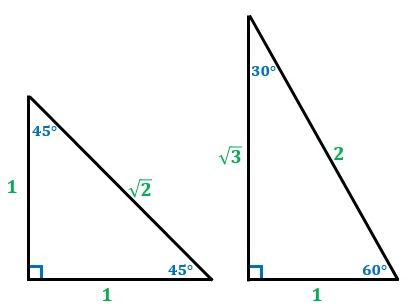
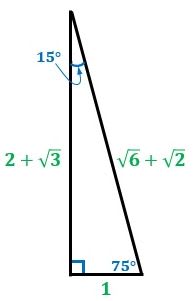
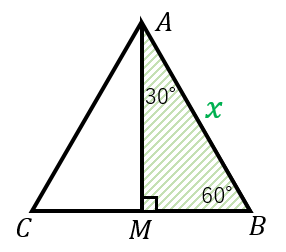
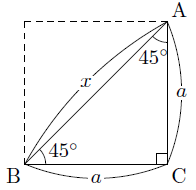
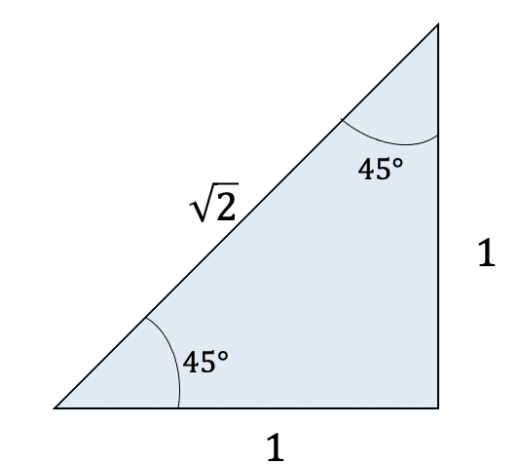
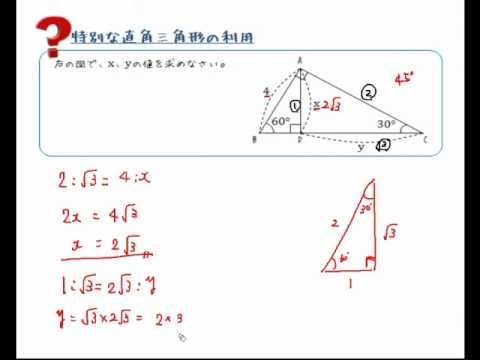
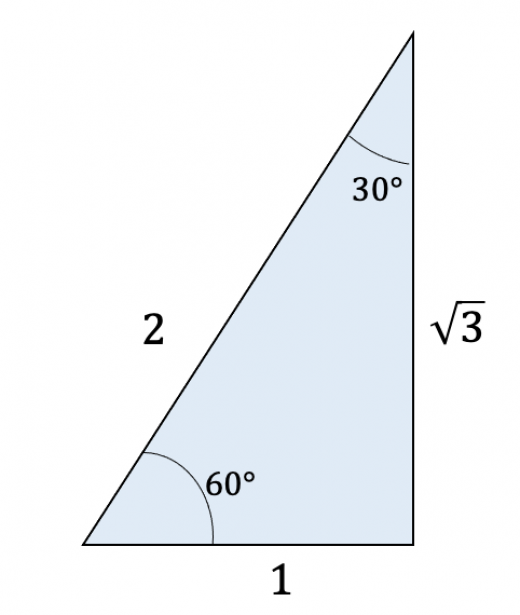
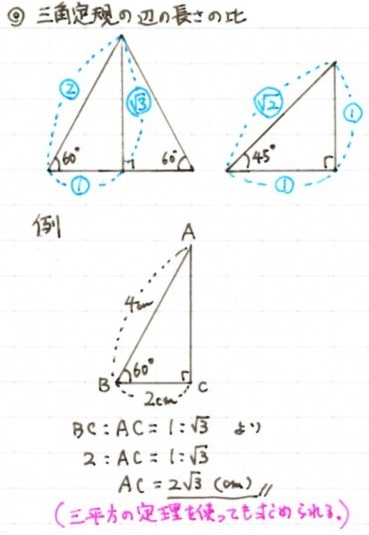
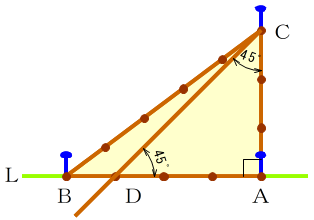
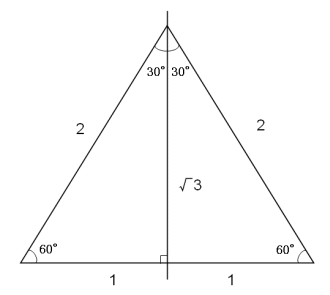
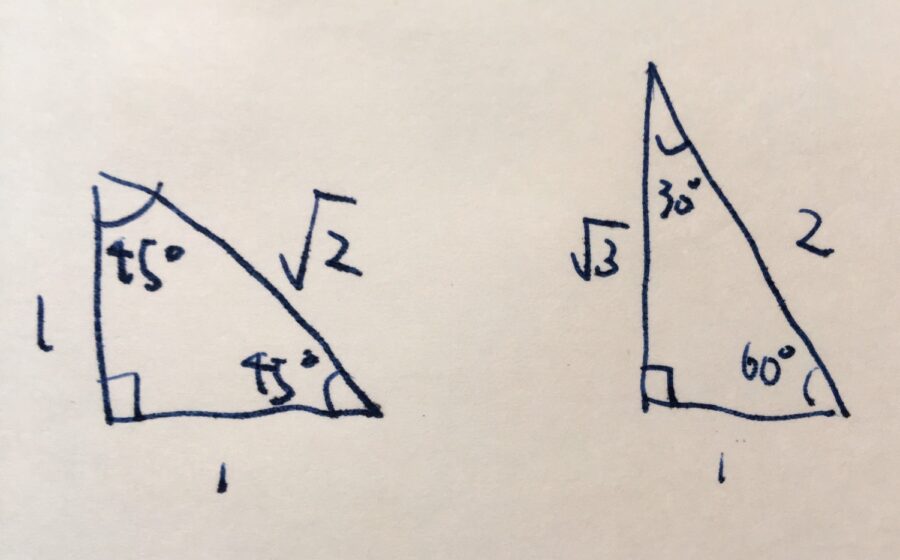
直角三角形 辺の比 求め方-この問題に答えるためには,辺の比が1: で,その間の角度が45°のときは,「1:1: の直角二等辺三角形になる」という中学校数学の基本が前もって分かっていなければなりません. このことに気 直角二等辺三角形の辺の比は になります。 この辺の比を覚えておくことで、底辺から斜辺の長さを求めたり、またその逆のことができます。 この章の最後の例題で確認してみてくだ
直角三角形 辺の比 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
 |  |  |
「直角三角形 辺の比 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「直角三角形 辺の比 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 | ||
「直角三角形 辺の比 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  | |
「直角三角形 辺の比 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「直角三角形 辺の比 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「直角三角形 辺の比 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  | |
「直角三角形 辺の比 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「直角三角形 辺の比 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |
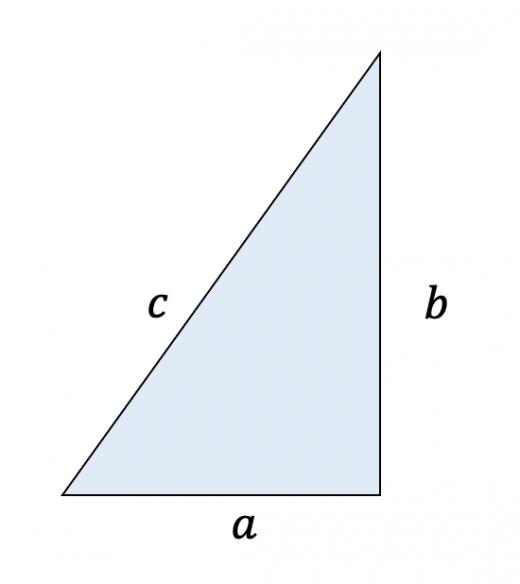
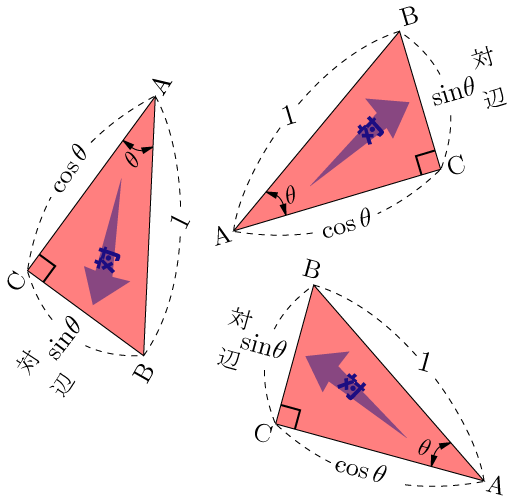
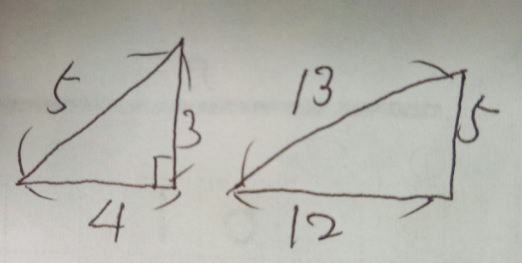
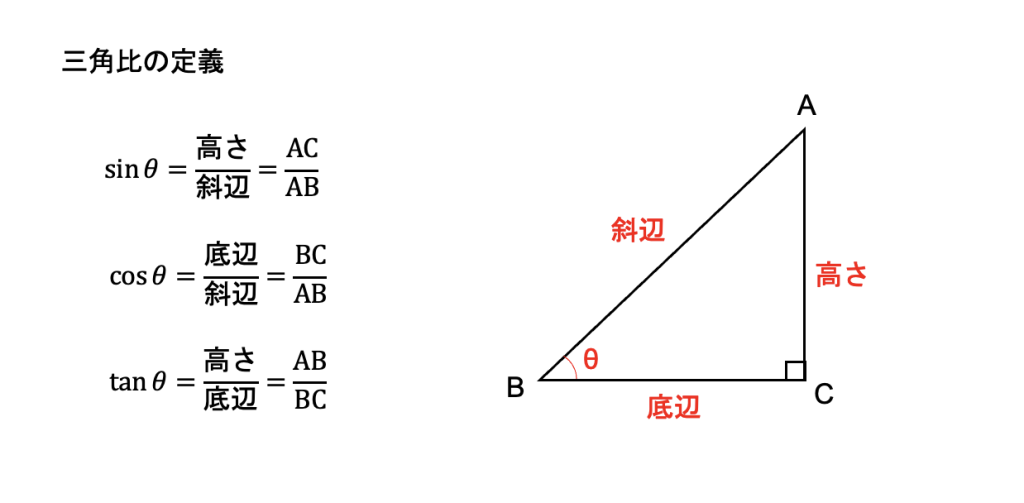
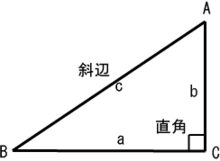
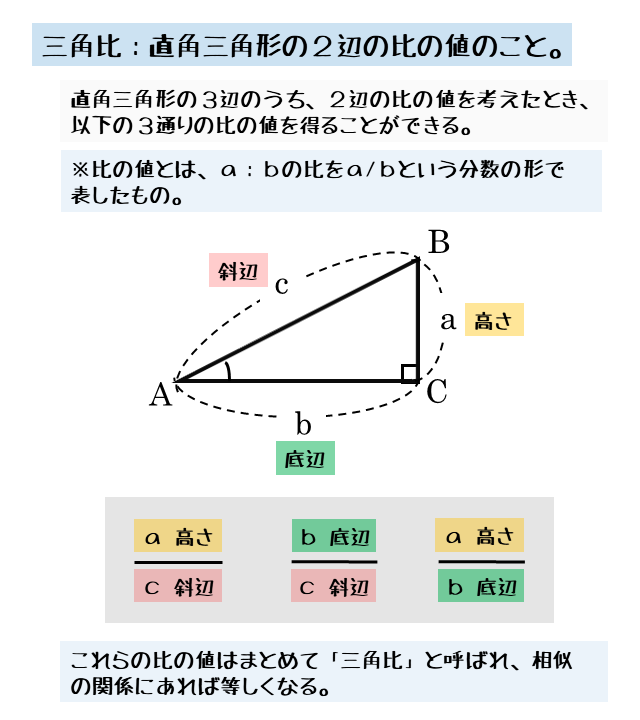
三角比の解説のポイント 斜辺を1として、三角形の辺の長さを考える 単位円への接続を意識する どの式で、何から何を求められるのか、付け加えて説明する 授業の進め方の例 ①相似 各辺が345の三角形って こんな感じで、ピタゴラスの定理にあてはまるよね! ピタゴラスの定理は、 直角三角形の3辺の長さは斜辺2 = 底辺2 高さ2 斜 辺 2 = 底 辺 2 高 さ 2 にな
Incoming Term: 直角三角形 辺の比, 直角三角形 辺の比 一覧, 直角三角形 辺の比 15度, 直角三角形 辺の比 角度, 直角三角形 辺の比 整数, 直角三角形 辺の比 求め方,




0 件のコメント:
コメントを投稿